OPEN-SOURCE SCRIPT
Boness 1964 Option Pricing Formula [Loxx]
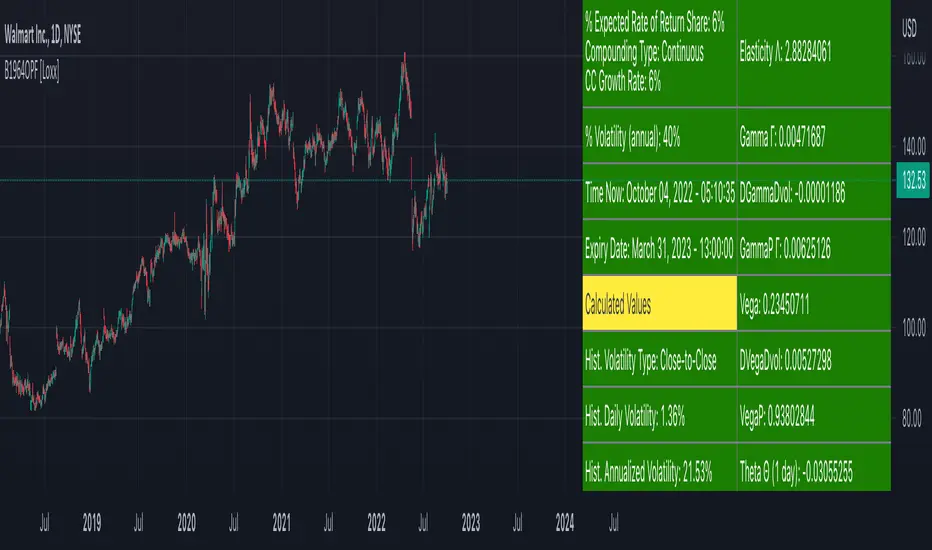
Boness 1964 Option Pricing Formula [Loxx] is an options pricing model that pre-dates Black-Scholes-Merton. This model includes Analytical Greeks.
Boness (1964) assumed a lognormal asset price. Boness derives the following value for a call option:
c = SN(d1) - Xe^(rho * T)N(d2)
d1 = (log(S / X) + (rho + v^2 / 2) * T) / (v * T^0.5)
d2 = d1 - (v * T^0.5)
where rho is the expected rate of return to the asset.
Analytical Greeks
Inputs
S = Stock price.
X = Strike price of option.
T = Time to expiration in years.
r = Expected Rate of Return
v = Volatility of the underlying asset price
cnd (x) = The cumulative normal distribution function
nd(x) = The standard normal density function
convertingToCCRate(r, cmp ) = Rate compounder
Things to know
Boness (1964) assumed a lognormal asset price. Boness derives the following value for a call option:
c = SN(d1) - Xe^(rho * T)N(d2)
d1 = (log(S / X) + (rho + v^2 / 2) * T) / (v * T^0.5)
d2 = d1 - (v * T^0.5)
where rho is the expected rate of return to the asset.
Analytical Greeks
- Delta Greeks: Delta, DDeltaDvol, Elasticity
- Gamma Greeks: Gamma, GammaP, DGammaDvol, Speed
- Vega Greeks: Vega , DVegaDvol/Vomma, VegaP
- Theta Greeks: Theta
- Probability Greeks: StrikeDelta, Risk Neutral Density, Rho Expected Rate of Return
Inputs
S = Stock price.
X = Strike price of option.
T = Time to expiration in years.
r = Expected Rate of Return
v = Volatility of the underlying asset price
cnd (x) = The cumulative normal distribution function
nd(x) = The standard normal density function
convertingToCCRate(r, cmp ) = Rate compounder
Things to know
- Only works on the daily timeframe and for the current source price.
- You can adjust the text size to fit the screen
Скрипт с открытым кодом
В истинном духе TradingView, создатель этого скрипта сделал его открытым исходным кодом, чтобы трейдеры могли проверить и убедиться в его функциональности. Браво автору! Вы можете использовать его бесплатно, но помните, что перепубликация кода подчиняется нашим Правилам поведения.
Public Telegram Group, t.me/algxtrading_public
VIP Membership Info: patreon.com/algxtrading/membership
VIP Membership Info: patreon.com/algxtrading/membership
Отказ от ответственности
Информация и публикации не предназначены для предоставления и не являются финансовыми, инвестиционными, торговыми или другими видами советов или рекомендаций, предоставленных или одобренных TradingView. Подробнее читайте в Условиях использования.
Скрипт с открытым кодом
В истинном духе TradingView, создатель этого скрипта сделал его открытым исходным кодом, чтобы трейдеры могли проверить и убедиться в его функциональности. Браво автору! Вы можете использовать его бесплатно, но помните, что перепубликация кода подчиняется нашим Правилам поведения.
Public Telegram Group, t.me/algxtrading_public
VIP Membership Info: patreon.com/algxtrading/membership
VIP Membership Info: patreon.com/algxtrading/membership
Отказ от ответственности
Информация и публикации не предназначены для предоставления и не являются финансовыми, инвестиционными, торговыми или другими видами советов или рекомендаций, предоставленных или одобренных TradingView. Подробнее читайте в Условиях использования.